
Основы теории стоимости денег во времени. Процессы накопления и дисконтирования
- 08.03.2015 21:16
- 6949
ОСНОВЫ ТЕОРИИ СТОИМОСТИ ДЕНЕГ ВО ВРЕМЕНИ
Измерение стоимости недвижимого имущества в денежной форме и тот факт, что его ценность определяется, как правило, текущей стоимостью будущих доходов от владения и использования недвижимости требует обращения к теории стоимости денег во времени, которая объясняет процессы определения будущей стоимости денег (накопление) и приведения денежных потоков к их текущей стоимости (дисконтирование).
Учитывая, что данные процессы основываются на эффекте сложного процента, основное внимание в этой главе будет уделено вопросам применения стандартных функций сложного процента в оценочных процедурах и объяснению их экономического содержания. В частности, будут рассмотрены шесть основных функций: накопленная сумма (будущая стоимость) единицы, накопление единицы за период, взнос в формирование фонда возмещения, текущая стоимость единицы (реверсия), текущая стоимость обычного аннуитета и взнос на амортизацию единицы.
Процессы накопления и дисконтирования
Как уже отмечалось, стоимость недвижимости выражается в денежной форме. Иными словами, деньги являются тем товаром, на который обмениваются права относительно объектов недвижимости. Но, как и любой другой товар, деньги должны обладать стоимостью, т.е. на соответствующем рынке, рынке капитала, можно за определенную плату взять деньги в пользование на определенный срок. На этом же рынке можно дать свои деньги в пользование на время, рассчитывая получить за это вознаграждение.
Это наглядно иллюстрируют банковские операции. При размещении денег на банковских депозитах, по сути, происходит их передача в пользование, а та процентная ставка, которую банк предлагает на вложенный капитал – плата за это пользование. И, наоборот, деньги, взятые в кредит, должны быть возвращены в банк в полном объеме вместе с определенным процентом, как платой за пользование этими деньгами.
В любом случае, сумма денег сегодня, которую называют текущей стоимостью, и сумма денег завтра, которую называют будущей стоимостью, будут отличаться на величину дохода по процентной ставке:
![]()
где FV - сумма, которая отражает будущую стоимость;
PV - сумма, отражающая текущую стоимость;
i - процентная ставка.
Рассуждая аналогичным образом, можно решить и обратную задачу, какую сумму PV необходимо вложить сегодня, чтобы в будущем получить определенную сумму FV при заданном уровне вознаграждения i:
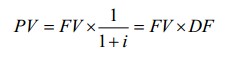
Эту задачу называют задачей дисконтирования, то есть приведения будущей стоимости в текущую стоимость, а коэффициент DF=1/(1+i), который при этом используется, называется коэффициентом дисконтирования.
Операции накопления и дисконтирования
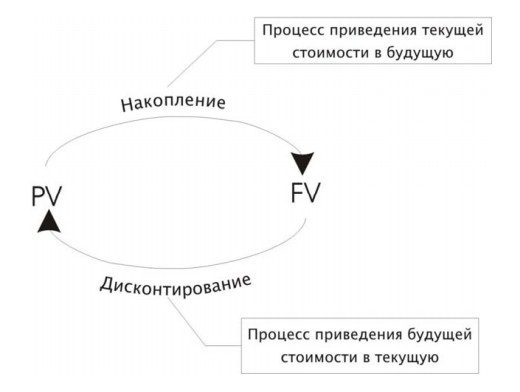
Таким образом, важнейшие операции, предоставляющие возможность сопоставить разновременные деньги - операции накопления и дисконтирования.
Накопление - операция приведения текущей стоимости в будущую.
Дисконтирование – приведение будущей стоимости в текущую.
На этих двух операциях выстроен финансовый анализ. Один из его основных критериев - процентная ставка, или соотношение чистого дохода и вложенного капитала. При выполнении операции накопления её называют ставкой дохода на капитал, при дисконтировании - ставкой дисконта.
Инвестирование в недвижимость очень похоже на ситуацию с пользованием деньгами. Вложение денег в покупку и/или строительство объектов недвижимости предполагает получение дохода в перспективе, а не сегодня. Такой отказ от текущего использования денег также требует своей оплаты – получение дохода на вложенный капитал. Таким образом, будущая стоимость любого объекта недвижимости будет больше текущей стоимости на величину этого дохода.
ПРИМЕР
Рассматривается проект инвестирования в строительство здания офиса. Прогнозный расчет показал: через год здание можно будет продать за 400 тыс. долл. Нужно определить, какую сумму стоит инвестировать в строительство сегодня, если приемлемый для инвестора уровень дохода составляет 15%.
Естественно, что ставка дохода на капитал, с которым инвестор может согласиться, будет определяться риском получения этой величины дохода. Чем выше риск достижения заданной величины дохода, тем больше должна быть норма оплаты за капитал, вложенный в строительство.
Приведенные рассуждения показывают, что текущая стоимость инвестиции будет равна 347826 долл.:
PV = FV× 1/(1 + i) = 400000 × 1/(1 + 0,15) = 347826
В данной задаче рассматривался один период, в конце которого предполагалось получить доход, т.е. ставка начислялась на первоначальный капитал. Если же получение дохода будет происходить в конце нескольких периодов (лет, месяцев), то начисление ставки будет осуществляться от суммы, накопленной в предыдущий период, т.е. по сложному проценту. В таком случае коэффициент дисконтирования для первого периода будет определяться как
DF1=1/(1+i)
В последующие периоды, если допустить, что i = const, он должен рассчитываться таким образом:
-
- для будущего денежного потока второго периода
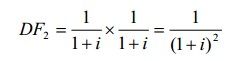
- для будущего денежного потока третьего периода
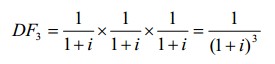
- для будущего денежного потока n - го периода
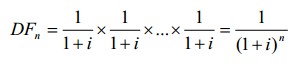
- для будущего денежного потока второго периода
Следует заметить, что на использовании эффекта сложного процента строятся многие задачи, решаемые в оценке недвижимости. Обычно процентная ставка при этом задается как номинальная годовая ставка. Если число периодов выражено не в годах, а в месяцах или кварталах, то процентная ставка также должна быть месячной или квартальной. С целью их определения номинальная годовая ставка должна быть разделена на соответствующее число периодов в году.
Разновременные денежные потоки, приведенные при помощи коэффициента дисконтирования к текущей стоимости, имеют свойство аддитивности. Это позволяет в общем виде представить текущую стоимость дисконтированного денежного потока за t периодов с принятым допущением о постоянном значении i следующим выражением:
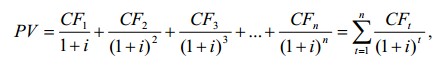
где Ct - денежный поток t-го периода
Это выражение называют формулой дисконтированного денежного потока. Формулу дисконтированного денежного потока при определенных условиях можно значительно упростить. Прежде всего, это касается одного из основных допущений, принятых в оценке недвижимости, о бесконечности дохода с земли. Если предположить, что величина ежегодного дохода будет постоянной, то текущая стоимость бесконечного потока равномерных постоянных поступлений при ставке дисконта, равной i, будет описываться геометрической прогрессией
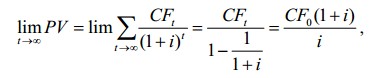
которую можно преобразовать в следующее выражение:
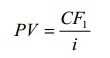
где С – денежный поток за период после текущего момента.
Это выражение – формула прямой капитализации.
В другом случае, если стоимость объекта определяется денежным потоком, ограниченным во времени, который сформирован серией равновеликих периодических поступлений (платежей), называемая аннуитетом, может быть использован фактор (коэффициент) текущей стоимости обычного аннуитета, разработанный Вильямом Инвудом (1771 – 1843):
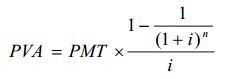
где PMT - величина одного из серии равновеликих периодических платежей или поступлений
i - процентная ставка (ставка дохода на капитал);
n - число периодов
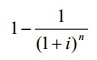
- фактор текущей стоимости обычного аннуитета.
Данный фактор - одна из 6 функций сложного процента, которые рассматриваются далее.

