Основы теории стоимости денег во времени. Стандартные функции сложного процента

17.03.2015 11:00

20890

Стандартные функции сложного процента

Применение стандартных функций сложного процента даёт возможность рассчитать величину любого из элементов, характеризующих распределенные во времени денежные потоки - стоимость, платеж, время, ставку, - при условии, что другие элементы известны.

Как правило, речь идет о 6 функциях сложного процента:

• накопленная сумма единицы(её будущая стоимость),
• накопление единицы за период,
• взнос в формирование фонда возмещения,
• реверсия (текущая стоимость единицы),
• текущая стоимость обычного аннуитета,
• взнос на амортизацию единицы

Поскольку эти функции применяют весьма широко и часто, разработаны стандартные таблицы, которые включают заранее рассчитанные факторы сложного процента. В данном контексте фактором называется одно из двух или более чисел, которые, будучи перемноженными, дают заданный результат. Все эти факторы созданы с применением базовой формулы (1 + i)n, дающей описание накопленной суммы единицы, и по сути, представляют собой производные от этого фактора.

Будущая стоимость единицы.

Будущая стоимость единицы – функция, которая определяет ее накопленную сумму спустя n периодов, если ставка дохода на капитал равна i. Функция подразумевает, что доход на капитал, полученный за период, вместе с первоначальным капиталом формирует базу, с которой будет определяться доход на капитал в следующий период.

Её рассчитывают по формуле:

где FV - будущая стоимость;
PV - текущая стоимость;
i - ставка дохода;
n - срок накопления (число периодов);
FVF(i;n) = (1 + i)n - фактор будущей стоимости единицы (накопленной суммы).

С помощью этой функции можно вычислить будущее значение денежной суммы, опираясь на ее текущее значение, размер ставки дохода на капитал и длительность срок накопления.

ПРИМЕР

В текущий момент стоимость земельного участка составляет 1000 долл., при уровне доходности 14%. Предполагается, что он будет продан через два года. При этом ни его характеристики, ни рыночные условия не изменятся. В данном случае будущая стоимость земельного участка станет равной 1300 долл.:

или, что одно и то же

Накопление единицы за период.

Накопление за период – функция, которая определяет будущую стоимость обычного аннуитета (то есть серии равновеликих периодических платежей и поступлений PMT) на протяжении n периодов при размере ставки дохода на капитал i.
Обычный аннуитет – это серия равновеликих периодических платежей и поступлений, причём первый из них производится в конце следующего, после текущего, периода. Если платежи производятся авансом, (в начале каждого периода), речь идёт об авансовом аннуитете.

Будущую стоимость обычного аннуитета рассчитывают по формуле:

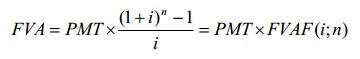
где FVA - будущая стоимость обычного аннуитета
PMT – величина одного из серии равновеликих периодических платежей или поступлений
i - ставка дохода;
n - число периодов;

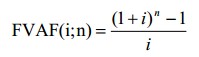
- фактор будущей стоимости обычного аннуитета.

ПРИМЕР

Нужно рассчитать будущую стоимость земельного участка, приобретенного при условии отсрочки платежа на полгода и компенсации 12% годовых. Платежи вносятся в конце каждого месяца  - равными суммами по 1000 долл. В таком случае будущая стоимость земельного участка окажется равной 6152 долл.:

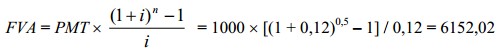
или, что то же самое

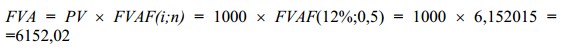
Взнос на формирование фонда возмещения.

Взносы на формирование фонда возмещения - функция, которой определяется величина платежей для обычного аннуитета, чья будущая стоимость через n периодов, при величине ставки i, равна 1.

Иначе говоря, с помощью функции взноса на формирование фонда возмещения можно определить размер равновеликого периодического платежа (регулярного дохода), нужного для накопления до конца установленного периода определенной суммы, с учетом накопленных процентов, при некоторой ставке дохода.

Расчет величины равновеликого периодического платежа осуществляется по формуле:

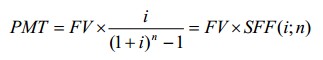
где PMT – величина равновеликого периодического платежа;
FV - будущая стоимость обычного аннуитета
i - ставка дохода;
n - число периодов;

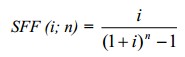
- фактор фонда возмещения
SFF (i;n) (фактор фонда возмещения) является обратной величиной фактора будущей стоимости обычного аннуитета:

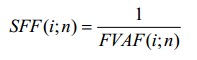
ПРИМЕР.

Нужно рассчитать величину ежегодных накоплений с целью равноценной замены существующего здания, которое приносит доход в 14%, с условием, что к окончанию периода экономической жизни (8 лет) затраты на замену здания составят 10000 долл. В данном случае величина ежегодных отчислений составит 755,70 долл.:

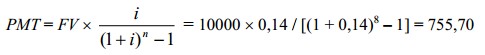
или

Текущая стоимость единицы (реверсии).

Текущая стоимость единицы (реверсии) – функция, которая определяет текущую стоимость будущей единицы, которую можно получить по истечении n периодов при заданной ставке дохода i. Данная функция позволяет осуществить оценку текущей стоимости дохода, который может быть получен от реализации объекта в конце периода при данной ставке дисконта.

Текущую стоимость единицы рассчитывают по формуле:

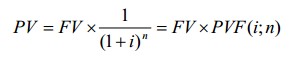
где PV - текущая стоимость;
FV - будущая стоимость;
i - ставка дохода (дисконта);
n - срок накопления (число периодов);

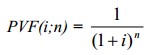
- фактор текущей стоимости единицы (реверсии).

В математическом смысле текущая стоимость единицы – это обратная величина функции ее будущей стоимости.

ПРИМЕР.

Требуется вычислить текущую стоимость земельного участка, который в конце года будет продан по цене 1000 долл. При ставке дисконта 10% в год текущая стоимость участка будет равной 909,09 долл.

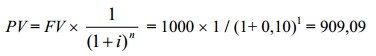
или

Текущая стоимость обычного аннуитета.

Текущая стоимость обычного аннуитета – функция, которая определяет текущую стоимость серии будущих равновеликих периодических платежей (поступлений) PMT на протяжении n периодов при ставке дисконта i. Вычисление осуществляют по формуле:

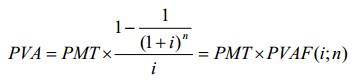
где PVA - текущая стоимость обычного аннуитета
PMT - величина одного из серии равновеликих периодических платежей (поступлений)
i - ставка дохода (дисконта);
n - число периодов

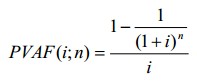
- фактор текущей стоимости обычного аннуитета.

Текущая стоимость обычного аннуитета может быть определена как сумма текущих стоимостей всех платежей:

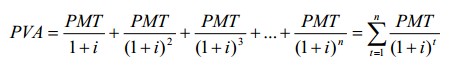
ПРИМЕР

Нужно определить текущую стоимость платежей по аренде, при условии, что земельный участок был сдан на три года, за ежегодную арендную плату 100 долл. Ставка дисконта равна 12%. Тогда текущая стоимость платежей составит 240,18 долл.:

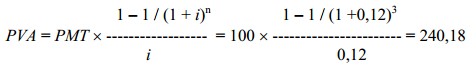
или

Взнос на амортизацию единицы.

Взнос на амортизацию единицы – функция, при помощи которой определяют величину регулярного платежа (поступления), обеспечивающего доход на капитал и его возврат при ставке дисконта i за n периодов. Взнос на амортизацию единицы можно рассчитать по формуле:

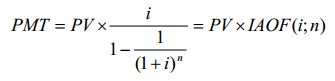
где PMT - величина платежа для обычного аннуитета;
PV - текущая стоимость единицы,
i - ставка дисконта (дохода);
n - срок накопления (число периодов);

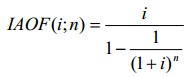
- фактор взноса на амортизацию единицы.

Эта функция, равно как и функция взноса на формирование фонда возмещения, даёт возможность определения платежа РМТ. Но в отличие от функции взноса на формирование фонда возмещения, связанной с платежом с целью накопления заданной суммы FV, функция взноса на амортизацию единицы имеет отношение к платежу, позволяющему вернуть заданную на текущий момент сумму PV. При этом платеж включает две составляющие: первая обеспечивает доход по заданной ставке i, вторая обеспечивает возврат капитала по норме возврата SFF(i; n) за n периодов.

Функция взноса на амортизацию единицы используется при определении регулярных равновеликих (аннуитетных) платежей в счет погашения кредита, если он выдан на некоторый период по заданной ставке по кредиту. При этом каждый платеж включает в себя и выплаты основной суммы долга, и начисленных процентов. Сами платежи при этом равновеликие, и от платежа к платежу соотношение доходной и возвратной составляющих меняется (уменьшается часть, с которой идёт выплата процентов, и увеличивается та часть, которая идёт на возврат принципала, то есть основной суммы кредита. То есть процент начисляется на невыплаченную сумму принципала и процентная ставка по кредиту, по мере его погашения, начисляется на меньшую сумму. Функция взноса на амортизацию единицы при этом обратна функции текущей стоимости обычного аннуитета.

ПРИМЕР.

Нужно рассчитать величину ежегодного дохода, который приходится на здание, которое будет эксплуатироваться в течение 5 лет, если его текущая стоимость равна 10000 долл., а ставка дисконта - 15%. При таких условиях размер ежегодного дохода составляет 2983,16 долл.:

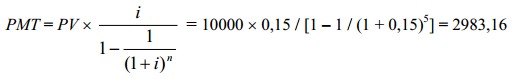
или, что одно и то же

Используя взаимосвязь факторов шести функций сложного процента, можно предложить представить логику их построения и экономический смысл в табличной форме.

Взаимосвязь и экономический смысл стандартных функций сложного процента

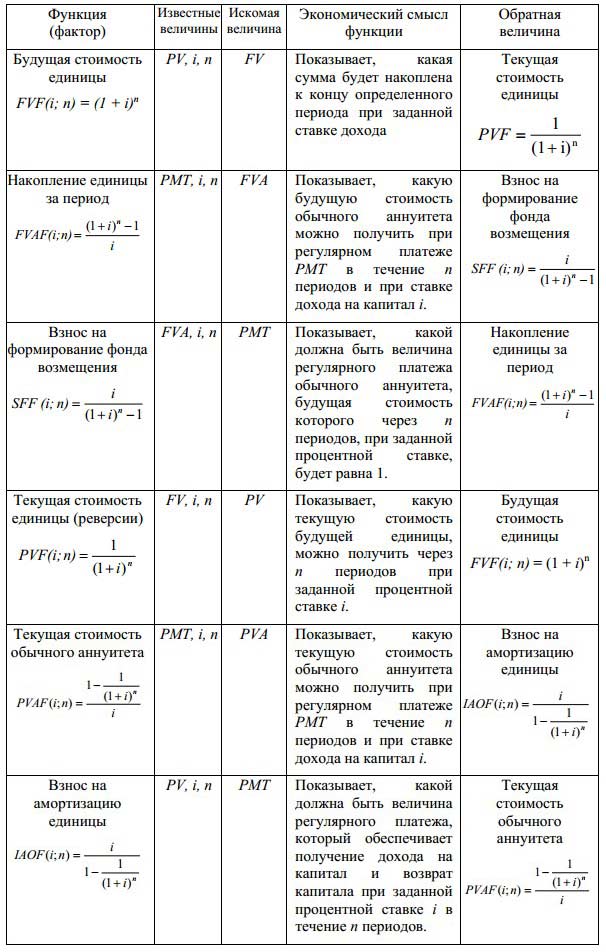
Резюме

В оценке недвижимости важную роль играет теория стоимости денег во времени. С ее помощью объясняется такой значимый для оценки процесс, как дисконтирование, отражающий взаимосвязь между понятиями текущая стоимость, будущая стоимость, регулярный доход, время, ставка дохода.

Данная взаимосвязь реализуется на основе использования 6 функций сложного процента, позволяющих определить искомую величину на основе умножения известной величины на соответствующий фактор, значение которого может быть вычислено или взято из таблиц 6 функций сложного процента. Это существенно облегчает выполняемые при оценке многочисленные расчеты.

• < Назад
• Вперёд >